A progressive algorithm for UMAP
Hyung-Kwon Ko, Jaemin Jo, and Jinwook Seo / 2020
PARTICIPANTS
- Hyung-Kwon Ko, Seoul National University
- Jaemin Jo, Seoul National University
- Jinwook Seo, Seoul National University
ABSTRACT
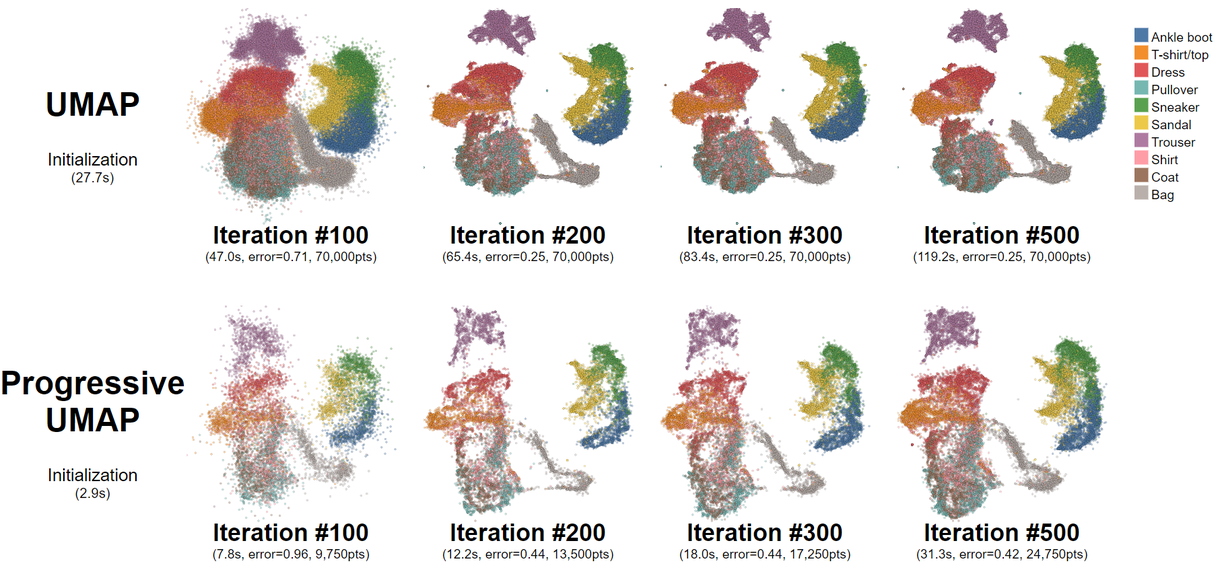
We present a progressive algorithm for Uniform Manifold Approximation and Projection (UMAP), Progressive UMAP. Based on the theory of Riemannian geometry and algebraic topology, UMAP is an emerging dimensionality reduction technique that offers better versatility and stability than t-SNE. Although UMAP is also more efficient than t-SNE, it still suffers from an initial delay of a few minutes to produce the first projection, which limits its use in interactive data exploration. To tackle this problem, we improve sequential computations in UMAP to be progressive, allowing people to incrementally append a batch of data points into the projection at the desired pace. In our experiment with the Fashion MNIST dataset, we found Progressive UMAP could generate the first approximate projection within a few seconds that sufficiently captured the important structures of high-dimensional data.